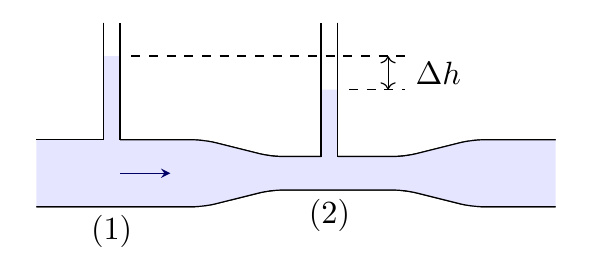
Το διαγώνισμα Α τετραμήνου 2021-2022 στις κρούσεις – ταλαντώσεις.
Ιστολόγιο
-
Τελικό διαγώνισμα φυσικής Γ Λυκείου
Ένα τελικό επαναληπτικό διαγώνισμα φυσικής σε όλη την (περικομμένη) ύλη του σχολικού έτους 2020-2021.
Καλή επιτυχία σε όλα τα παιδιά!
-
Μικρή επανάληψη στο Στερεό Σώμα
Ερωτήσεις και ασκήσεις (μερικές συνδυαστικές) για επανάληψη στο Στερεό, όπως έχει διαμορφωθεί μετά την περικοπή της ύλης το 2021…
-
Φθίνουσα – εξαναγκασμένη ταλάντωση
Μία μελέτη της φθίνουσας και της εξαναγκασμένης ταλάντωσης με το πακέτο SymPy της Python είναι στο github
https://github.com/gpapadem/jupyterNotebooks/blob/main/Oscillations-Dumped-Driven2.ipynb
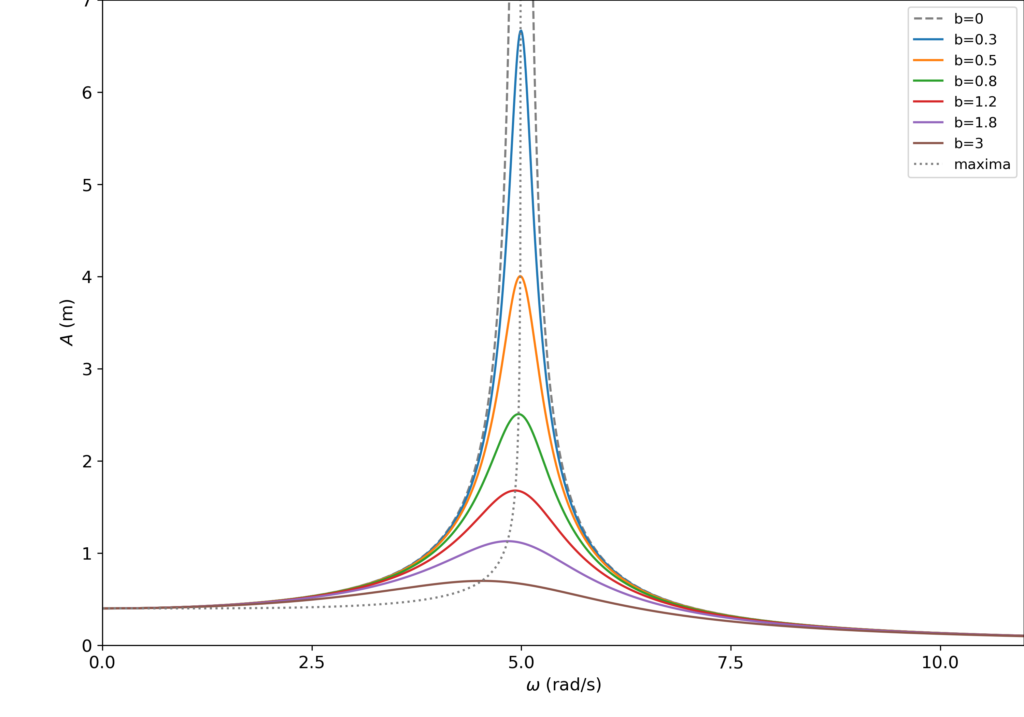
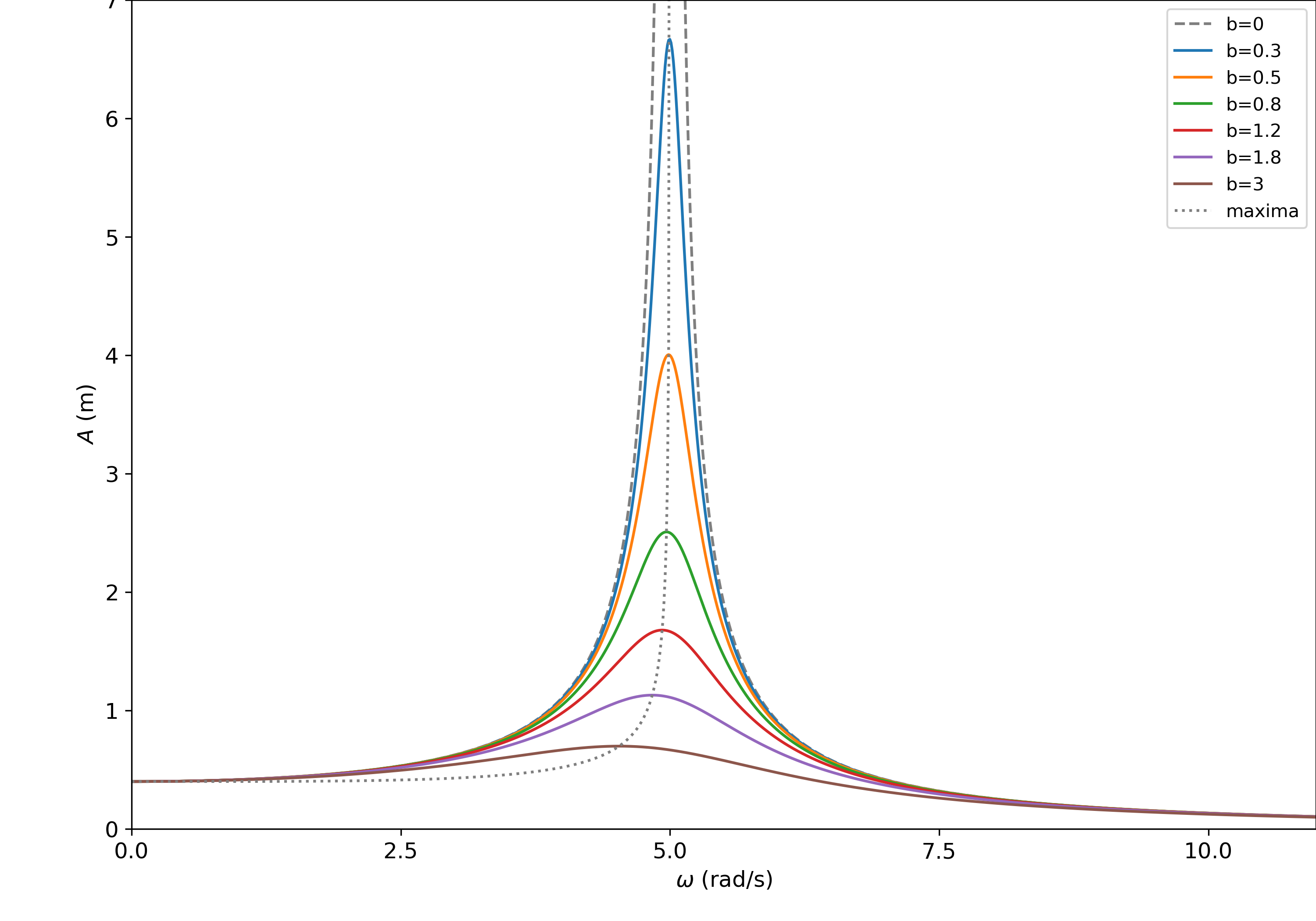
Διάγραμμα του πλάτους (σε σταθερή κατάσταση) ως συνάρτηση της συχνότητας διεγέρτη για διάφορες τιμές της σταθεράς απόσβεσης b, με δύναμη διέγερσης της μορφής F=10συν(ωt) (SI) σε σύστημα με ιδιοσυχνότητα 5rad/s. Η εστιγμένη (dotted) καμπύλη παρουσιάζει της θέσεις των κορυφών για τις διάφορες τιμές της σταθεράς b.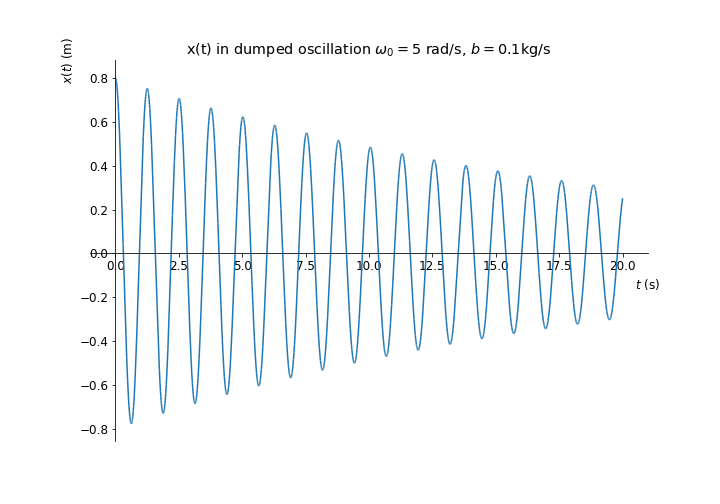 
Φθίνουσα ταλάντωση μάζας m=1kg, σε ελατήριο σταθεράς k=25N/m με σταθερά απόσβεσης b=0.1kg/s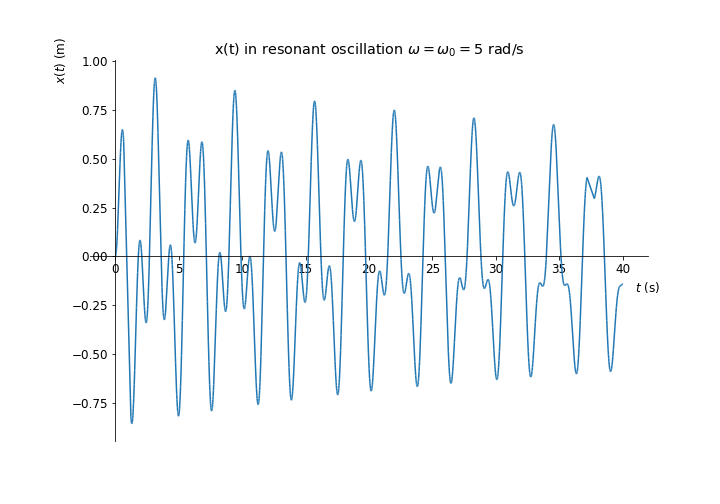 
Αρχική (μεταβατική) φάση της εξαναγκασμένης ταλάντωσης σε συντονισμό με b=0.05kg/s, δύναμη διέγερσης της μορφής F=10συν(ωt) (SI) και τα υπόλοιπα στοιχεία ίδια με την προηγούμενη εικόνα. -
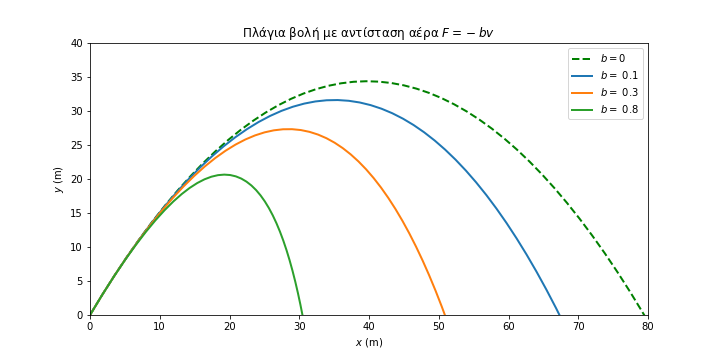
Πλάγια βολή με αντίσταση αέρα
Σε μία πλάγια βολή επιδρά και μία δύναμη αντίστασης
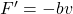(σε ένα απλοποιημένο μοντέλο). Μπορούμε να λύσουμε αριθμητικά τη διαφορική εξίσωση για την ταχύτητα
και![\[\frac{d}{dt}v_y(t) = - \frac{b}{m}v_y(t) - g\]](https://gpapadem.sites.sch.gr/wp-content/ql-cache/quicklatex.com-a9ca7e80d65b7e6bbe078096bc349331_l3.png "Rendered by QuickLaTeX.com")
με το odeint του πακέτου scipy της python.![\[\frac{d}{dt}v_x(t) = -\frac{b}{m}v_x(t)\]](https://gpapadem.sites.sch.gr/wp-content/ql-cache/quicklatex.com-79d452d9b5b8618b31bf0a5017770a2e_l3.png "Rendered by QuickLaTeX.com")
Εκτός από τις ενδιαφέρουσες γραφικές παραστάσεις με το matplotlib μπορούμε να δημιουργήσουμε και animation από τις λύσεις των διαφορικών μας…
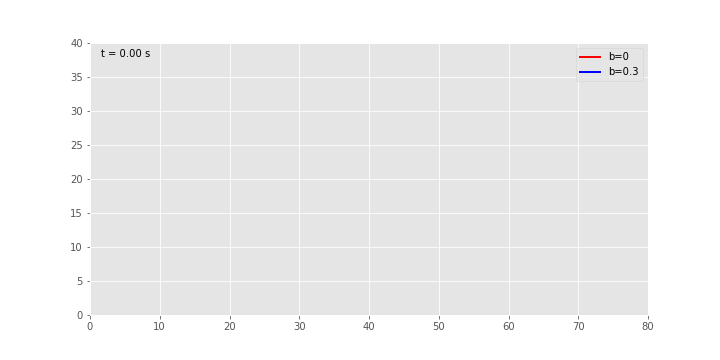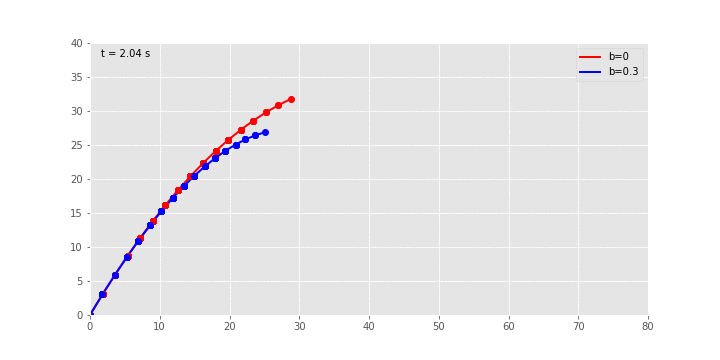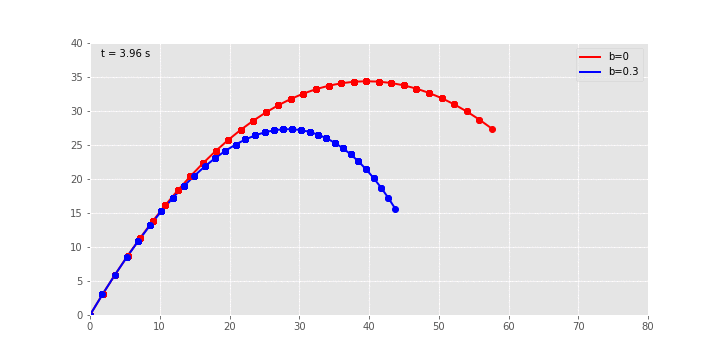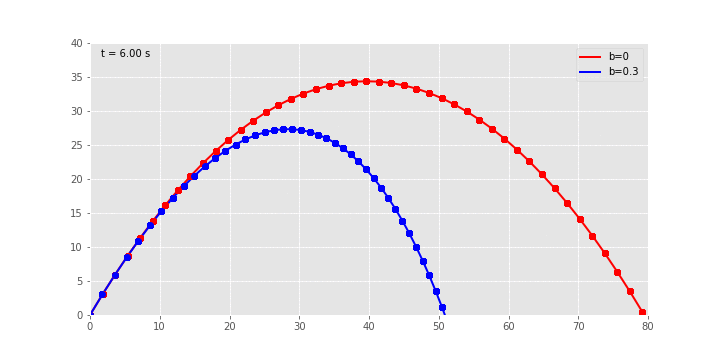
Στην παραπάνω gif εικόνα φαίνονται οι τροχιές για πλάγια βολή με αρχική ταχύτητα
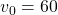m/s και γωνία 
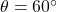για δύο τιμές της σταθεράς αντίστασης 
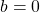και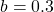 
kg/s αντίστοιχα. Το animation έγινε με την FuncAnimation() του matplotlib πακέτου…Το πλήρες jupyter notebook με τον κώδικα βρίσκεται στη σελίδα μου στο github.
-
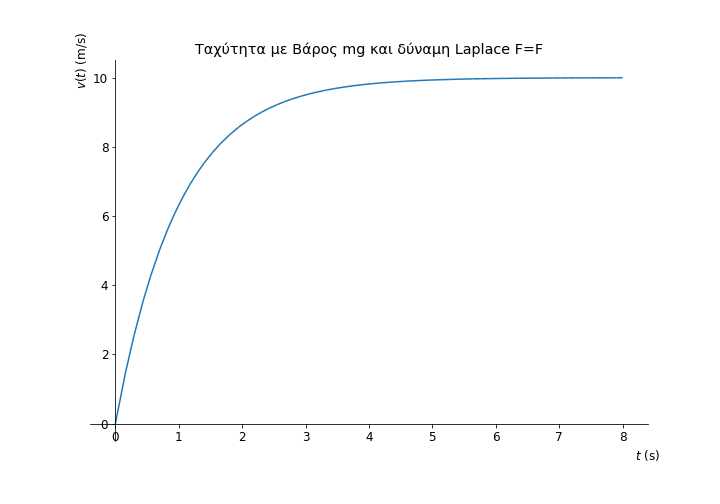
Jupyter Notebook για ράβδο που πέφτει μέσα σε ΟΜΠ
Η γλώσσα προγραμματισμού python έχει πολλά επιστημονικά πακέτα – εργαλεία που προσφέρουν απίστευτες δυνατότητες στους περιστασιακούς προγραμματιστές (εμάς)…
Ένα από αυτά είναι το sympy (Symbolic python), ένα εργαλείο για συμβολικές μαθηματικές πράξεις, άλγεβρας, ανάλυσης κτλ. Με το sympy μπορείς να λύσεις αναλυτικά (συμβολικά) διαφορικές εξισώσεις, όπως π.χ. στο Mathematica.
Παρακάτω είναι μία λύση της κίνησης μίας οριζόντιας ράβδου που αφήνεται να πέσει μέσα σε ομογενές οριζόντιο και κάθετο σε αυτήν μαγνητικό πεδίο, όπου υπολογίζουμε την ταχύτητα, την επιτάχυνση και την μετατόπιση (και άλλα) λύνοντας τη διαφορική εξίσωση της κίνησης.
Για την ταχύτητα της ράβδου η λύση της διαφορικής δίνει:
![\[ \displaystyle v{\left(t \right)} = \frac{R g m + e^{B^{2} l^{2} \left(- \frac{t}{R m} +\frac{\log{\left(- R g m \right)}}{B^{2} l^{2}}\right)}}{B^{2} l^{2}}\]](https://gpapadem.sites.sch.gr/wp-content/ql-cache/quicklatex.com-e11971db7a1e8a1d32da3e303d328333_l3.png "Rendered by QuickLaTeX.com")
https://github.com/gpapadem/jupyterNotebooks/blob/main/RodFallingInMagneticField.ipynb
-
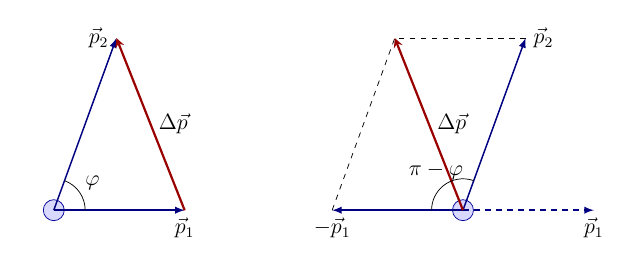
Ορμή και δύναμη
Μερικές σελίδες για την ορμή
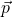, τη μεταβολή της ορμής \Delta\vec p και τη σχέση της με τη συνισταμένη δύναμη \Sigma \vec F… -
Σύνθεση ταλαντώσεων – Βασική θεωρία
Η βασική θεωρία στη σύνθεση ταλαντώσεων.
